MNIST – Regularized Logistic Regression

Hello guys

Sometimes when we train our algorithm, it becomes too specific to our dataset which is not good. Why? Because the algorithm must be able to classify correctly data never seem before too. So today, I’ll show you a way to try to improve the accuracy of our algorithm.

Overfitting

The problem described in the introduction is know as overfitting. Overfitting occurs when the algorithm becomes to specialized to the training data. It means that during the training it will be able to classify very well (even 100%) but it will perform poorly with new data. More information about overfitting can be read in wikipedia.

The image below depicts what happens when we overfit:

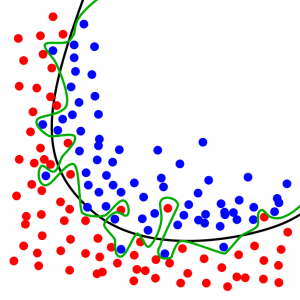Figure 1 – Overfitting problem

As you can see, the green line is when we overfit. It tries to split all datapoint exactly as they should be splitted. This occurs when we have too much features for example.

Regularization

Regularization is the technique used to avoid overfitting. Simply put we’ll add a term in our function to be minimized by gradient descent.

Currently our logistic regression use the following gradient descent:

\displaystyle \frac{\partial error}{\partial a_n} = -\frac{1}{m}\sum_{i=1}^{m} x_n \left ( h(x) -  y) \right ) \text {\hspace{10 mm} \small eq. 1}

In order to add regularization we just need to add:

\displaystyle \frac{\partial error}{\partial a_n} = -\frac{1}{m}\sum_{i=1}^{m} x_n \left ( h(x) -  y) \right ) +  \frac{\lambda*a}{m}\text {\hspace{20 mm} \small eq. 2}

With some manipulations we’ll find:

\displaystyle new \textunderscore a = a - \alpha [\frac{1}{m}\sum_{i=1}^{m} x_n \left ( h(x) -  y) \right ) + \frac{\lambda*a}{m}] \text {\hspace{15 mm} \small eq. 3}

\displaystyle new \textunderscore a = a(1 - \alpha \frac{\lambda}{m}) - \alpha \frac{1}{m}\sum_{i=1}^{m} x_n \left ( h(x) -  y) \right) \text {\hspace{13 mm} \small eq. 4}

The term

\displaystyle a(1 - \alpha \frac{\lambda}{m})

is a number between below 1 and intuitively we can see that it will reduce the value of $new \textunderscore a$ by some amount on every iteration.

Please don’t confuse $a$ parameter with $\alpha$ . I’m sorry but Katex renders the letter a and alpha very similar.

Features scaling

For this post, we’ll rescale our features as well using the following formula (as discussed here):

x_i = \frac{\displaystyle x_i - x_{min}}{\displaystyle x_{max} - x_{min}}

Results

Splitting the dataset as 10k for training and 32k for testing, I run to tests:

No regularization: $\lambda = 0$ , 50 iterations, learning rate $\alpha = 0.6$ , we get 87.50%.
Regularization: $\lambda = 450$ , 50 iterations, learning rate $\alpha = 0.6$ , we get 87.75%.
Regularization: $\lambda = 3000$ , 50 iterations, learning rate $\alpha = 0.6$ , we get 77.53%. (Underfitting)

Submiting to Kaggle our algorithm regularized we finally got 87.642% which is close to our 87.75%.

Of course, this algorithm can be improved and tuned, but you got the idea! You can find the source code here.

Next time we’ll start looking at neural networks, but I have to confess that it will take a little to prepare the post!

Bye and I hope to see you soon!

Marcelo Jo

Marcelo Jo is an electronics engineer with 10+ years of experience in embedded system, postgraduate in computer networks and masters student in computer vision at Université Laval in Canada. He shares his knowledge in this blog when he is not enjoying his wonderful family – wife and 3 kids. Live couldn’t be better.

Marcelo Jo